/**
* 221. Maximal Square
* Given an m x n binary matrix filled with 0’s and 1’s,
* find the largest square containing only 1’s and return its area.
* Example 1:
* Input: matrix = [[“1″,”0″,”1″,”0″,”0”],[“1″,”0″,”1″,”1″,”1”],[“1″,”1″,”1″,”1″,”1”],[“1″,”0″,”0″,”1″,”0”]]
* Output: 4
* interesting question to calculate size of squares
*/
Matrix questions are frequently asked and they have similar patterns. Hence, answering this question here.
See my solution here: https://github.com/zcoderz/leetcode/blob/main/src/main/java/frequent/medium/MaximalSquare.java
The question is asking for the maximum square area in a matrix. This can be calculated via:
- Create a new two-dimensional array to calculate the square size per cell. Set the size of this array one greater than the matrix size so as to make the matrix traversal simple (getting prior row, column and diagonal is simplified).
- Loop over the rows and columns once and calculate 1 seen around the current cell – one column to left, one row above, and prior diagonal.
- If the current cell is 1, taking the minimum value from the 3 surrounding cells (see #2) and adding 1 to it to get the current square length.
- Keep track of the maximum square length seen so far
- Max Area is max square length multiplied by itself.
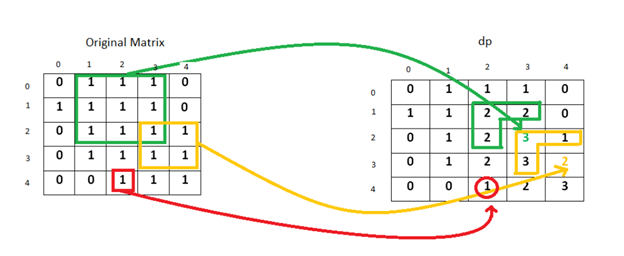
The following image copied from leetcode’s solution explains the above algorithm visually. See leetcode’s detailed solution here : https://leetcode.com/problems/maximal-square/solution/
Here is the code:
public int maximalSquare(char[][] matrix) {
if (matrix.length==0) return 0;
int cols = matrix[0].length;
//allocate a new array, set it to be 1 row and col more than the orig , this makes offset calculations easier
int [][] matrixCopy = new int[matrix.length+1][cols+1];
for (int[] ints : matrixCopy) {
Arrays.fill(ints, 0);
}
int maxSquares = 0;
//start with row and col 1
for (int iRow =1; iRow <= matrix.length; iRow++) {
for (int iCol =1; iCol <= cols; iCol++) {
//look at the original matrix by subtracting 1 from row and col
if (matrix[iRow-1][iCol-1] != '1') continue;
//you only need the 3 cells indicated below, this can done via using
//the copy as one dimensional array than 2 dimensional.
//you can get left , down from the one dim array. for diag left you can keep track it in a
//variable.....
int leftCell = matrixCopy[iRow][iCol-1];
int downCell = matrixCopy[iRow-1][iCol];
int digLeft = matrixCopy[iRow-1][iCol-1];
//your max Sq is min of adjacent sq values + 1 for the current
//draw this on a white board and it will make sense
int maxSq = Math.min(Math.(leftCell, downCell), digLeft);
maxSq++; //increment max square value
matrixCopy[iRow][iCol] = maxSq; //set the calculated value in current matrix copy
maxSquares = Math.max(maxSq, maxSquares); //update max
}
}
return maxSquares*maxSquares;
}