/**
*287. Find the Duplicate Number
* Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.
* There is only one repeated number in nums, return this repeated number.
* Example 1:
* Input: nums = [1,3,4,2,2]
* Output: 2
* Example 2:
* Input: nums = [3,1,3,4,2]
* Output: 3
*/
See my solution here: https://github.com/zcoderz/leetcode/blob/main/src/main/java/frequent/medium/FindDuplicateInArray.java
You can solve the problem via adding the data to a set and checking which value repeats.
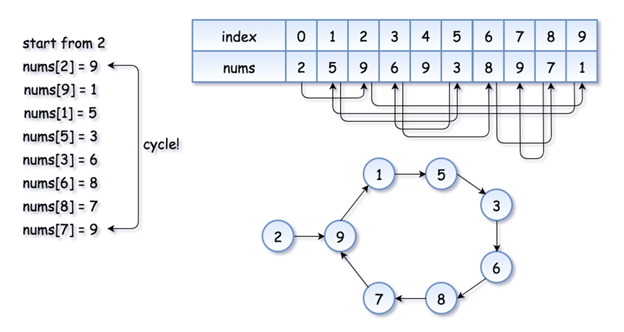
Below is another way to solve the problem that uses Floyd’s Tortoise and Hare (cycle detection approach). Mentioning it here since this concept repeats often.
Since the values in array index are from 1 to n, but with a single repeat. You can treat the repeat value as start of a cycle. Then the problem becomes solving for where the cycle starts.
The Floyd approach is based on below:
- S: starting index
- F: distance between starting index and where the cycle starts
- C: distance until the cycle repeats
- M: intersection point of the slow and fast pointer (see description below)
Approach is that you start two pointers from the starting index, with one pointer going twice as fast as the other. Since one pointer is going twice as fast as the other at some point they will intersect, per above the intersection point is M. Then you can deduce an equation that 2 * (F+M) = F + nC + M , where n is the number of iterations around the cycle that the fast pointer loops. This equation can be simplified to F+m = nC.
Given F = nC – m, you can start two pointers, going at same rate. One at S and the other at m. After going through distance F, one of them will be at distance F and the other at F + m. Since F + m = nc, the second pointer would be at nC+F which is same as F.
See visual (borrowed from leetcode explanation) which emails the above concept in a nice diagram.
Here is the code:
public int findDuplicate(int[] nums) {
int i = 0, j = 0;
while (i != j || (i == 0)) {
i = nums[i];
j = nums[j];
j = nums[j]; //move j twice as fast as i
}
//j based on above is at point m based on above logic
i = 0; //move i to start
while (i != j) {
i = nums[i];
j = nums[j];
}
return i;
}